サーブの打点と入る最高速度2023-02-22

テニスのサーブはサイドアウトのミスより、ネットかオーバーのミスの方が多いと思います。これは当然、サーブを入れる為の上下方向の許容範囲が狭いからです。もしボールの軌道が直線だと仮定すると、ギリギリサーブを入れるには打点は3ｍくらい必要。だから「サーブはスピンを掛けなければ入らない」等とよく言われます。

確かにサーブを入れるのは難しいですが、よく考えてみてください。ボールが直線軌道で飛ぶという前提は、重力の影響を無視しています。実際にはボールの軌道は重力で引っ張られて山なり（所謂「放物線」）になるので、そこまで条件は厳しくありません。

そこで今回は、打点の高さが何mなら最高何km/hのサーブが入るのか？を検証したいと思います。尚、スピンの影響や空気抵抗（正確には「効力」）による減速と言ったエアロダイナミクスは無視します（次回以降にやる予定）。皆さんが高校までに習った筈の三角関数とニュートン力学だけで計算していきます。

サーブの軌道計算

下図は3D CADでテニスコートの図と寸法を描いたものです。先ずは上述の直線軌道でギリギリ入る打点を計算します。（もう結論が描いてありますが💦）

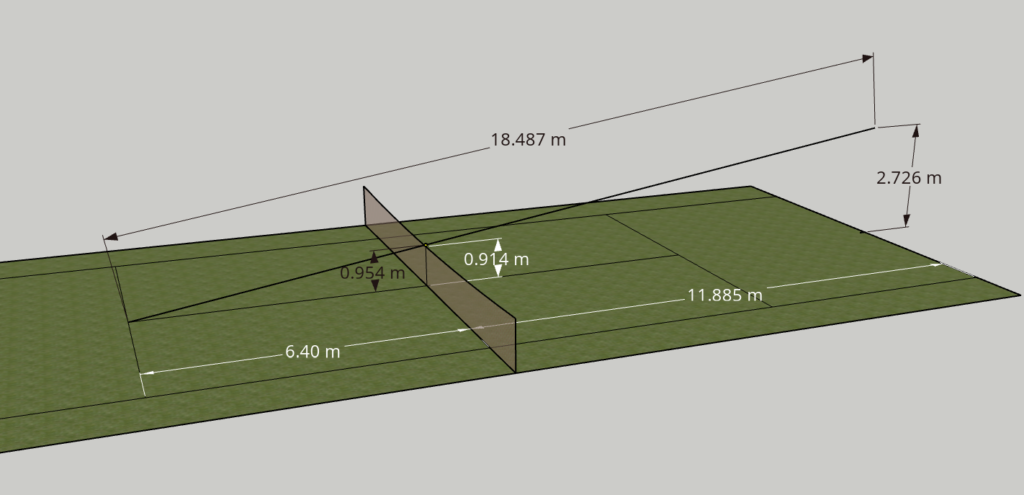
前提条件として、話を簡単にする為に、打点の位置はベースラインのセンターマークの真上とし、一方の落下ポイントは相手のサービスラインとセンターラインの交点とします。すると当然、ボールはネット中央の一番低い部分（0.914ｍ）の上空を通過します。つまり一番入れやすく到達時間が短いケースです。

次に、テニスボールのサイズは直径6.54～6.86cm、半径だと3㎝ちょいです。なので若干余裕を見て、ボールの中心からネット上端まで4㎝（0.04m）あれば、レットせずに通過出来る筈です。その場合、地面から見たボールの（中心の）高さは、ネットの高さ（0.914m）に0.04m足して0.954mとなります。

これで高さ0.954ｍ（ネット上通過位置）、底辺長さ6.4m（ネットから相手のサービスラインまでの距離）の直角三角形が出来ました。この三角形の斜線をサーバーのベースラインまで伸ばしていけば、打点の高さ（H）が判ります。関係式は；

6.4/0.954 = (6.4+11.885)/H

となるので、これを変形すると；

H = (6.4+11.885)*0.954/6.4 = 2.7256 ≒ 2.7 (m)

となります。よく言われる3ｍには及びませんが、2.7mの打点で打つには日本人としてはかなり高身長（手もそれなりに長い）な男性でないと無理でしょう。

因みに僕は、身長も腕の長さも日本人男性の平均以下ですが、打点の高さを測ったら、2.4ｍ弱しかありませんでした(;´д｀)トホホ。道理で速いサーブが入らない訳だ(‘◇’)ゞ　皆さんもご自分の打点の高さを測ってみてください。

測り方は、僕の場合は伸縮出来る孫の手があったので、先ず自分のラケットのグリップエンドからスウィートスポットまでの長さに調整しました（約50㎝でした）。勿論この棒は自撮り棒や指示棒でも良いと思います。何なら50㎝の物差しでも。

そして壁の傍に立ち、その棒をラケットのように持ってサーブのインパクトの形を作り、棒の先端の高さにある何らかの目印を壁上に見つけます。後はコンベックス（鉄製の巻き尺）で地面からその目印までの高さを測ります。

僕の場合は、偶々その高さが部屋の天井付近だったので判り易かったですが、そんなに都合よい目印が無かったり、そもそも天井の高さが足りないかも知れません。その場合は、分かり易い目印の高さになるように棒の長さを調整し、後でラケットのグリップエンドからスウィートスポットまでの長さと比較し、差分を足し引きしたら良いのではないでしょうか？

重力を考慮したサーブの軌道

という訳で、皆さんの打点の高さはどうでしたか？もしそれが思ったより低くても、ドッカン・フラットサーブを諦めるのはまだ早いですよw

冒頭で述べたように、スピンが全く掛かっていなくても、重力によってボールの軌道はドンドン下向きになり、全体として山なりの軌跡（所謂「放物線」）を描きます。逆に言えば、軌道が直線になるのは速度が無限大の時だけです。速度が有限なら、速いほどボールは直線軌道に近くなり、遅いほど下に向かって垂れ下がるような軌道になります。

では実際にボールがどんな軌道を描くのか計算してみましょう。

先ずニュートン力学のおさらいですが、地球上にある物体は皆、地球の重心に向かって引き寄せられます。つまり空中にあるモノは「落ちる」訳ですが、地球がモノを引っ張り続けるので、その速度はドンドン増していきます。

この時の加速度は「重力加速度」(G)と呼ばれ、どんな物体でも一定です（つまり質量が大きな物体ほど、強い力で地球に引っ張られる）。具体的には毎秒9.8m/sづつ速度が増していきます（G=9.8m/s^2）。という事は、ボールの落ち初め（サーブのインパクト）から着地迄の時間が判れば、ボールが直線軌道から外れて「落ちる」距離が判るのです。

では先ず、ボールの速度をV、ボールの飛行距離をL、ボールの飛行時間をTとすると、次の式が成り立ちます。

L = VT

距離＝速度ｘ時間ですから自明ですね。正確には飛行距離Ｌは放物線（2次関数）の長さですが、計算がややこしいのでざっくり直線軌道の長さとして計算していきます。

冒頭のテニスコートの図に戻って頂き、大きい方の直角三角形を考えます。この三角形の高さ、つまり打点の高さですが、2.7mは現実的ではないので、キリが良い2.5mとします（これなら多分日本人男性の平均くらいでしょう）。一方、底辺の長さはベースラインから相手のサービスラインまでの距離＝(6.4+11.885)m です。するとこの三角形の斜線が飛行距離Lになるので、ピタゴラスの定理を使うと次の式が得られます；

L^2 = 2.5^2 + (6.4+11.885)^2

ここから飛行距離Lを計算すると

L = 18.455 ≒ 18.5(m)

となります。次にボールの初速Vを仮に180km/h（=50m/s）とすると、飛行時間Tは;

T = L/V = 18.5 / 50 = 0.37 (s)

となります。最短コースとは言え、0.4秒足らずで到達するんですね。トッププロでもセンターサーブを警戒していなければ反応できない時間でしょう。

では、落下距離はどうなるかというと、経過時間とボール速度のグラフの面積に一致します。一般的には積分で求めますが、この場合は等加速度運動なので、底辺が経過時間(0.37s)、高さが最終速度(0.37*9.8m/s)である三角形の面積が落下距離になります。つまり落下距離をHgとすると；

Hg=T*T*G/2=(0.37*0.37*9.8 )/2 = 0.67(m)

となります。勿論これは打点から67㎝下がった位置という意味では無く、同じ打ち出し角の直線軌道と比べて最終的に（相手のサービスラインの位置で）67㎝下がるという意味です。

因みに、67㎝というと180㎞/hも出てる割には落ちてると思いませんか？ところがこれを「67㎝の高さからテニスボールを落としたら0.37秒で着地」と言い換えたら「まあそんなもんかな」と思うのではないでしょうか？重力って意外と強力ですね。

関数グラフでボールの軌道を描画する

次は、打ち出し角を一定にして初速を変えていった時にボールがどんな軌道になるのかを、関数グラフで表現します。

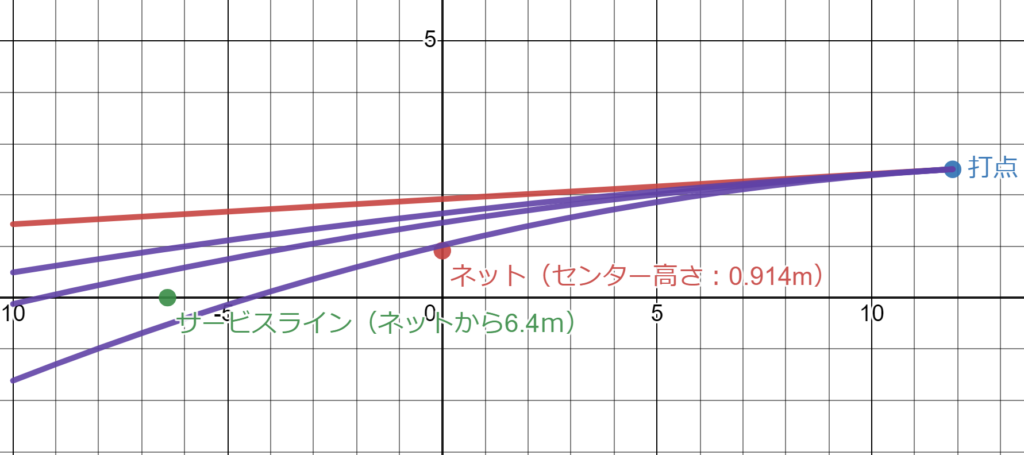
上のグラフはテニスコートを真横から見た図で、X軸は地面、Y軸はコートの真ん中、つまりネットの位置です。右の「打点」から向かって左方向にサーブを打つとします。

先ず直線軌道のグラフですが、打点の高さをh、打ち出し角度（水平から何度下がったか）をa、とすると、グラフの傾きはtan a (タンジェントa)となります。また、x = 0の時のyの値は、打点高さｈから11.85（ネット ー ベースライン間）* tan a を引いた値になります。従ってグラフの関数は次の通りです。

y=h – 11.85 * tan a + x * tan a

これに対して現実の放物線は、重力加速度Gの分だけ高さ（つまりyの値）が減少します。この減少幅（落下距離）は、インパクトからの経過時間 t を底辺とし、最終速度を高さとする直角三角形の面積 s に等しいので次の式が成り立ちます。

s = t * t * G / 2

ここでtを求める為に移動距離 d を直線軌道の距離に近似すると；

d = (6.4+11.885)/cos a

となります。更に経過時間 tを速度Vや変数xで表すと；

t = {(6.4+11.885)/cos a} /V * (x-11.885)/(6.4+11.885)

となり、このtを上述の落下距離の式に代入すると；

[{(6.4+11.885)/cos a} /V * (x-11.885)/(6.4+11.885)]^2*G/2

となり、直線軌道の関数からこの落下距離を引くと；

y=2.5 – 11.85 * tan a + x * tan a – [{(6.4+11.885)/cos a} /V * (x-11.885)/(6.4+11.885)]^2 * 9.8/2

という関数が出来ました。この式を（単位は適宜揃えます）グラフ描画ソフトに入力し、速度Vを100, 140, 180km/hとした場合のグラフが上と下の図です。

先ず上のグラフは、打ち出し角度a を100km/hの時にギリギリネットを超えるように調整しています。そうすると、100km/hの時はサービスラインの内側に余裕で入っているのに、他の速度では全てオーバーしています。

そこで相手のサービスライン地点の高さを見ると、100km/hでは直線軌道（速度∞）の場合と比べ2m以上低くなっているのに対し、100km/hと140km/hの場合の比較だと高低差は1mちょいになります。更に140km/hと180km/hでは（同じ40㎞/h違いなのに）50㎝くらいしか高低差がありません。

理由はこのグラフが速度の2次関数になっているからです。つまり初速が速くなるほどサーブの難易度が「加速度的」に上がっていくわけです。

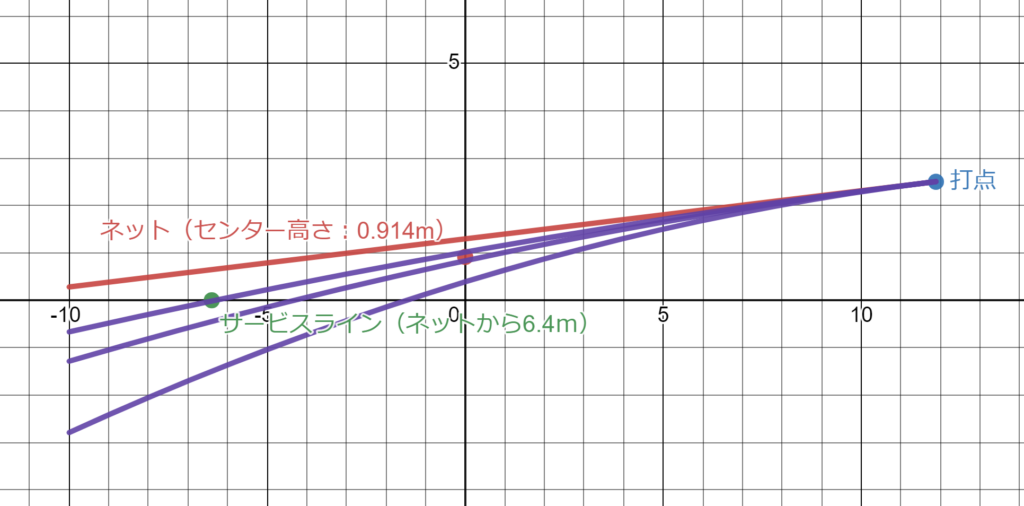
次に打ち出し角度をもう少し下げていき、180km/hのサーブがネット上ギリギリを通過する程度に打ち出し角を下げるとギリギリ入りました（上図）。ですので当記事の結論は；

打点の高さが2.5mであればフラットサーブは約180km/h迄なら入る

となります。しかしネットの上スレスレを通って粗サービスライン上に落ちるのですから、文字通り寸分の狂いも許されません。これでは喩えジョコビッチ並みに正確なショットの持ち主でも現実的なサーブとは言えません。

因みに、ボールの初速を徐々に変化させていくと軌道がどう変化するか、アニメーションで表現してみました。今回は判りやすいように打ち出し角度は水平にしたので、下に向かうベクトルは全て重力によるものです。

画面左端の数式の中で「v=○○」と表示されているのがボールの初速です（範囲は0~200km/h）。初速が0の時は当然真下に落ちるだけですが、速度が上がるにつれ軌道が持ち上がり、200km/hの時には大分水平に近くなっているのが判ります。

ここで注目して欲しいのは、ボール速度の変化率は一定にしてあるのに、速度が高くなる程、軌道の変化がゆっくりだという事です。これが何を意味するかというと、高い速度域のサーブを少々減速しても、入れやすさは殆ど変化しないという事です。つまり180km/hのサーブが余裕で入る打点で打てる人なら、200km/hで打っても確率は左程落ちないという事です。テニスにとってプレーヤーの身長（正確には高さ方向のリーチ）が如何に重要かという事ですね。予想された事とは言え、低身長の僕には絶望的な結論になってしまいました😿

気を取り直して次回は、ボールがネット上を通過する時の高さ（x=0の時のyの値）を決め、打ち出し角を逆算したいと思います。そしてその結果から落下位置も判るので、結局何km/hまでならサービスボックスに入るのか算出できます。