平均律と純正律2009-01-02
この記事を最初に公開したのはもう20年以上前ですが、何度も修正を加えながら現在(2025年/7月)も更新中です💦
最初は単に僕の好奇心で色々調べた結果を纏めた記事でしたが、その後「平均律は汚れている、美しい純正率に戻そう」みたいな主張が散見されるようになり、それは違うでしょと。その後何年かかけて、そうした純正律至上主義みたいなのは減りましたが、代わりに近年は文章と周波数の数値だけとか、下手すると純正律のチューニングの仕方みたいな記事が検索上位に入っています💦
そこで本記事では(と言うか元からそうなんですが)どういう理屈で周波数(比)を決めたのかと、それによって実際の音はどう響くのかをオーディオで示したいと思います。
音律と音階
先ず、ここで説明するのは「音律」であって「音階」ではありません。音階(スケール)とは「ヨナ抜き」(ペンタトニック)とか、ブルース・スケールとか、琉球音階とか、或いは「教会旋法」の各モードとか、音の数も各音の周波数比も違うものです。
一方音律とは、同じ8音の西洋音階の中で、微妙に違うチューニングのバリエーションです。古くは古代から、何故それほど多くの音律が生まれたかと言うと、ある音の組み合わせでは綺麗に響いても、別の組み合わせだと気持ち悪く響いてしまうからです。ここでいきなり結論めいた事を言うと、そうした試行錯誤の結果、最終的に落ち着いたのが平均律という訳です。
平均律(equal temperament)とは
まず前提として、古今東西どの音階も周波数が1:2の音程すなわち「オクターブ」があります。この音程は良くハモるというより(音色は異なるが)同じ音に聞こえます。これは基音が違うだけで倍音がほぼ同じような配列なので当然です。従って、このオクターブを一単位として、その中をどのように分割するかが「音階」です。
さて本題ですが、所謂「平均律」はこのオクターブを12等分します。よって正確には「12平均律」と呼びます。

ただ「等分」と書きましたが、上図のように周波数が等間隔で並んでいる訳ではありません。等間隔に聞こえる音は周波数の「比」が一定なのです(等比数列)。つまりオクターブを12等分した音程とは、12回かけたら2になる数値(2の12乗根)を周波数比とする音程です。具体的な数値で表すと2^(1/12)=1.059…となります。
これは喩えると、年利5.9%で預金(とか投資)をすると12年後には元本の2倍になるのと同じ理屈です。因みに近年の超低金利に慣れていると、こんな高金利は有りえないと思うでしょうが、バブル以前の定期預金はこのくらい普通でした( ´艸`)
脱線しましたが、平均律では1:1.059の周波数比が最小単位でこれを「半音」とします。そして、半音2個分(1.059^2=1.122)の音程を「全音」と呼びます。ご存知のようにダイアトニックスケールは、E-F間とB-C’間のみが半音で、残りは全て全音です。つまり12音で均等に分割し、そのうち7個の音を使うのが平均律のドレミ…です。
平均律の長所と短所
上述の定義から、どの音程も半音の整数個分(べき乗分)ですから、度数が同じならどこをとっても全く同じ音程(同じ響き)です。また、どんな調で演奏しても音同士の相対関係は同じなので、完全な平行移動が出来るという訳です。
反面、オクターブ以外はどの音程も簡単な整数比にはならないので、和音が若干にごる事になります。また現実問題として、平均律は調弦が非常に難しい事も挙げられます。何故なら、デジタルチューナーが無い時代は、唸りが無い音程=純正音程(下記)を重ねて調律する他ありませんが、平均律の純正音程はオクターブしかないからです。これが中々平均律が普及しなかった理由だと思います。
純正律(Just intonation)とは
「純正」とは「(2つの音の周波数が)単純な数比である」と言う意味です。従って純正律とは、(出来るだけ多くの)純正な音程で構成される音律です。平均律が究極の妥協点だとすれば、純正律は和音至上主義と言えるでしょう。
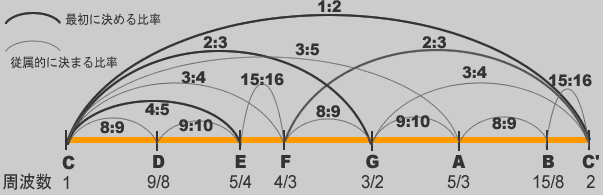
上図が各音の周波数の関係ですが、何だか分数パズルのようで一目瞭然だともいます。
一応文章で説明すると、まずオクターブの関係C-C’は当然1:2です。1:2に次いで単純な数比は2:3ですが、ここでCから周波数2:3で上がった音をGとします。反対にC’から2:3で下がった音をFとします。
そこでC-F間を計算すると3:4であり、同様にG-C’間も3:4になります。また、FとGの比率を計算してみると、8:9になります。案外すっきりした比率なので、これを全音(一音)としておきます。
次は、C-E間を4:5に設定します。そして、C-D間は上記の全音を採用し8:9とします。すると結果的に隣のD-E間は9:10となります。あれ?同じ全音なのにC-DとD-Eでは微妙に違いますね。このように純正律では長短2種類の全音があるのです。長い方(8:9)を大全音と呼び、短い方(9:10)を小全音と呼びます。
次に隣のE-F間を計算してみると15:16で、これが半音になります。しかし、この半音の2個分(2乗)は大全音(8:9)にも小全音(9:10)にもなりません。つまり、純正律の半音は全音の半分ではないのです。言うなれば「半端な音程」みたいな意味でしょうか。よって、例えばC♯とD♭は平均律では全く同じ音ですが(異名同音)、純正律では微妙に違う音になります。#や♭は元の音からちょい上がったとかちょい下がった音と言う意味なのです。
さて、残るはAとBです。Gから小全音上がった音をAとすると、C-A間は3:5とキリが良い数字になります。更にAから大全音あがった音をBとすると、B-C’間は15:16で先ほどの半音と同じです。めでたしめでたし。
純正律(Just intonation)の長所と短所
ご覧のように、純正律の音程は整数比の関係なので、当然綺麗にハモリます。ところがそうでない音程も存在します。例えば、完全5度の筈のD-Aの周波数比を計算すると27:40と言う複雑な数比になります。
なぜ同じ5度音程なのに場所によって比率が異なるのか?それは、C-G間をC-D-E-F-Gにばらして考えると、大全音+小全音+半音+大全音で構成されています(これが純正)。しかし一方、D-A間は小全音+半音+大全音+小全音なので、大全音が一個少なく代わりに小全音が1個多いのです。
後述しますが、このD-A間の「少し小さめの5度」は聴いてはっきり判るほど濁ります。平均律の5度のような微妙な濁りではありません。Ⅱmコードがかなり濁ってしまうという事は、ジャズやポップスは勿論、所謂クラシック音楽でも古典派以外はほぼ使えないでしょう。よく純正律の欠点として転調の困難さが挙げられますが、同じ調の音同士でも問題がある組み合わせが必ず存在するのです。
平均律と純正律の周波数比較
それでは両音律の各音の周波数を比較してみましょう。下表はダイアトニックの周波数で、グラフは半音階の周波数です。
| 純正律 | 平均律 | |
| C | 1 | 1 |
| D | 1.125 | 1.122 |
| E | 1.25 | 1.26 |
| F | 1.333 | 1.335 |
| G | 1.5 | 1.498 |
| A | 1.667 | 1.682 |
| B | 1.875 | 1.888 |
| C’ | 2 | 2 |
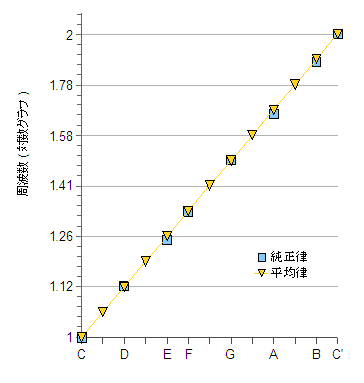
グラフの縦軸(周波数)は対数になっており、聴覚上の音高と見た目の音高を一致させています。よって、各音の間隔(数比)が等しい平均律の音階は直線上に並んでいます(黄色の三角)。一方、各音の間隔が不揃いな純正律(青の四角)は、微妙ですが直線上にはありません。特に純正律のEやAは平均律との差が大きくなっています。
一方和音(周波数比)の観点からすると、E音が両者で結構違うということは、平均律のC-E音程が純正3度(周波数比4:5)から結構乖離している事になります。平均律は3度が汚いと言われる所以はここにありそうです。Aもかなりずれていて、これはCから6度(C’から短3度)の音程です。一方、F(4度)やG(5度)では両者さほど変りません。この程度であれば、聴覚上殆ど影響がないと思われます。
という訳ですが、よく考えると平均律は純正音程を全く考えていない割に、2:3や4:5と言った単純な周波数比にかなり近い音程が偶々出来ていると思いませんか?これが例えば10平均律や16平均律だと、そうはいきませんから。
平均率 vs 純正律聴き比べ
さていよいよ、実際に音を聞き比べてみます。まずはC(ハ長調)の音階(所謂、ドレミファ・・・)です。まずは平均律から;
もちろん何の変哲もない、聴きなれた音階です。次は、純正律の音階です。
どうですか?気持ち悪い?良く分からない?よく聞くと、Eが低いのが判るでしょうか?そしてAも低いと思います。ただ、同じ音を平均律と純正律で交互に比較すると違いがハッキリ判ると思いますが、夫々の音階を弾いた場合は、純正律は不均等だから明らかに違和感があるというほどでは無いかもしれません。
次にコードを弾いたらどうなるでしょうか?この楽譜の通り、ダイアトニックのトライアドを弾いてみました。

先ずは平均律から。
これもよく聴く和音ですね。では純正律だとどうなるでしょうか?ハモリは純正律が得意な筈なんですが・・・
ん?これは!・・・最初のC(ドミソ)は平均律の場合より音のまとまりが良いと思いませんか?そして次のDm(レ ファ ラ)は打って変わって怪しい響きですよね。これが上述の狭い5度です。他の音は微妙といえば微妙なんですが、僕はEm,F,GそしてBdimが綺麗に響いているように聴こえました。
次の実験は真ん中の3度を抜いた5度音程、所謂「パワーコード」です。半音も含めて全ての組み合わせを試しました。

楽譜にするとこんな感じです。何番目の音がどうだったかで覚えていてくださいね^^;
これは微妙に濁っているというか唸っている感じがするんですよね。ピアノのサンプリング音のせいかもしれませんが。なお9番目のG#は一瞬唸ってるように錯覚しますが、発音タイミングが揃ってないようです。あとは、半音で均等に上がっていく感じです。次は純正律です。
これは!トライアドより粗が目立ちますね。矢張り3番目のD-Aは明らかに音痴です。次のD#も怪しい。E、Fは良くて、次のF#(7番目)もかない怪しい。9番目のG#は上と同じ発音タイミングがずれてますが、音程も何だか怪しい。12番目のBとF#の組み合わせはとても綺麗に聴こえます。
皆さんはどう感じたでしょうか?平均律の唸りはまあ慣れればOKレベルですが、純正律の(純正音程以外の)唸りはちょっと耐えられないのではないでしょうか?
よく「平均律は転調のし易さと引き換えに、美しい和音を失った」といった意見を見かけますが、対する純正律は「転調がしにくい」どころの騒ぎではありません。有体に言えば、純正律は、一部の純正音程(和音)と引き換えに、その他の酷い音程という代償を払ったというのが正確でしょう。
楽器の種類と音律
さて、現在は平均律が主流とは言うものの、部分的に純正律の楽器も沢山あります。
まず、金管楽器はその構造上、2:3(5度)が純正です。金管楽器はピストンを何も押さない(トロンボーンならスライドを一番短くした)状態で、ド-ソ-ド-ソ‐ド・・・の音程を唇の緊張度で弾き分けます。これは楽器の固有振動数の整数倍の音が出ている訳ですから、まさしく「純正」の5度です。
また、バイオリン族のようにフレットがない弦楽器は演奏者が自由に音の高さを変えられるので、異なる弦同士の相対調弦次第で、原理的にはどんな音階/音律でも演奏可能です。何処まで本当か判りませんが、バイオリニストはピアノの音律に違和感を覚えると言いますし、優れたバイオリニストはC♯とB♭の違いをきちんと弾き分け られると言います。
ただ合奏では、各楽器が平均律ではないのにキー(基音)が違うわけですから、原理的には唸るような音程があちこちで生まれる筈です。その場合、他のパートの音と濁らないように音高を調整しながら演奏しているのだと思います。そもそもビブラートを掛ければ、うなりは大分誤魔化せますし💦
純正律の鍵盤楽器
因みに、もし純正律の鍵盤楽器を作るとどうなるでしょうか?平均律ならC#とD♭は同音で黒鍵になっていますが、純正律では違う音なので、この黒鍵を2つに分割する必要があります。そんな楽器がこちらです。
動画の説明では、この楽器は2022年に作られたもので、チューニングは純正律ではなく「1/4コンマのミーントーン」だそうです。が、必要なキーは揃ってるので、純正律でチューニングすれば純正律チェンバロが出来る筈です。しかし、このように製作も演奏も大変な楽器が普及する筈もなく、微妙なピッチを演奏によって変えられない鍵盤楽器は、平均律に収斂していったのだと思います。
良い響き=簡単周波数比?
さて、これまでは「2つの音の周波数比が単純であるほど響きが良い」という前提で書いてきましたが、果たして本当でしょうか?
数学的には整数比の音程からほんの僅かでもずれると(僅かであればあるほど)、超複雑な比率になります。しかし、人間が調律したり演奏する音程が、常に完璧なんてありえないですよね。そうすると、演奏中に音が強烈に濁ったり唸ったりする筈ですが、実際にはそんなことは起きません。
何故なら、純正音程から僅かにズレた程度では、唸りがゆっくり過ぎて聞き取れないからです。また、通常楽器の音には基音以外に多くの周波数成分が含まれており、アコースティックギターやピアノでは減衰過程でこの倍音成分が急速に変化します。一方、弦楽器や管楽器など音を伸ばせる楽器は大抵ビブラートをかけるので、やはり濁りをごまかせます。
更に言えば、ピアノの中高音部は音量を増やす為に一つの音に複数の弦が張ってありますが、それらは全く同じ高さに調律しているわけではありません。僅かに(数セント単位で)チューニングをずらして、かすかな唸りを作り出しています。その方が音が華やかに聴こえるからです(ヤマハの解説)。これは、コーラスエフェクト(原音にピッチを僅かにずらした音を混ぜて広がりを出す)と同じ理屈ですね。
純正律は本当に使われたのか?
詳しくは別の記事にするつもりですが、歴史的に純正律は最古の音律でもなければ、逆に平均律を除く最新の音律でもありません。最古はピタゴラス音律(2:3だけ何度も繰り返す)で、これをベースに中世~ルネサンス期のヨーロッパで様々な音律が考案されました(所謂「古典音律」)。
有名な話ですが、J.S.バッハの「平均律クラビア曲集」は平均律を示すのか否かの論争があり、現在では粗否定されているようです。そもそも原題の意味は「平均律」ではなく「よく調律された(well temperament)」という曖昧なものです。バッハ的には全ての調で演奏しても破綻し難い「いい感じの調律」みたいな意味で言ったのかも知れません。よって実際には当時の古典調律の中で比較的平均律に近いものが選ばれたと思います。
じゃあ純正律は何時使われたのか?という疑問が湧きます。これについてはググってもChatGPTでもほぼ同じ答えが返ってきます。実は上述のピタゴラス系の古典音律を「純正律」と呼んでいるようなのです。従って、この記事で説明した本来の意味での純正律は恐らく概念的なもので、実際の音楽ではほぼ使われなかったのではないか?と私は考えています。